Regular ideal
In mathematics, especially ring theory, a regular ideal can refer to multiple concepts.
In operator theory, a right ideal 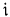 in a (possibly) non-unital ring A is said to be regular (or modular) if there exists an element e in A such that
in a (possibly) non-unital ring A is said to be regular (or modular) if there exists an element e in A such that 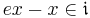 for every
for every 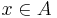 . (Jacobson 1956)
. (Jacobson 1956)
In commutative algebra a regular ideal refers to an ideal containing a non-zero divisor[1]. (Larsen & McCarthy 1971, p.42) This article will use "regular element ideal" to help distinguish this type of ideal.
A two-sided ideal 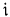 of a ring R can also be called a (von Neumann) regular ideal if for each element x of
of a ring R can also be called a (von Neumann) regular ideal if for each element x of 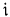 there exists a y in
there exists a y in 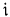 such that xyx=x. (Goodearl 1991, p.2) (Kaplansky 1969, p.112)
such that xyx=x. (Goodearl 1991, p.2) (Kaplansky 1969, p.112)
Finally, regular ideal has been used to refer to an ideal J of a ring R such that the quotient ring R/J is von Neumann regular ring. [2] This article will use "quotient von Neumann regular" to refer to this type of regular ideal.
Since the adjective regular has been overloaded, this article adopts the alternative adjectives modular, regular element von Neumann regular, and quotient von Neumann regular to distinguish between concepts.
Contents |
Properties and examples
Modular ideals
The notion of modular ideals permits the generalization of various characterizations of ideals in a unital ring to non-unital settings.
A two-sided ideal 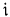 is modular if and only if
is modular if and only if 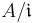 is unital. In a unital ring, every ideal is modular since choosing e=1 works for any right ideal. So, the notion is more interesting for non-unital rings such as Banach algebras. From the definition it is easy to see that an ideal containing a modular ideal is itself modular.
is unital. In a unital ring, every ideal is modular since choosing e=1 works for any right ideal. So, the notion is more interesting for non-unital rings such as Banach algebras. From the definition it is easy to see that an ideal containing a modular ideal is itself modular.
Somewhat surprisingly, it is possible to prove that even in rings without identity, a modular right ideal is contained in a maximal right ideal[3].
- Examples
- In the non-unital ring of even integers, (6) is regular (
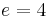 ) while (4) is not.
) while (4) is not. - Let M be a simple right A-module. If x is a nonzero element in M, then the annihilator of x is a regular maximal right ideal in A.
- If A is a ring without maximal right ideals, then A cannot have even a single modular right ideal.
Regular element ideals
Every ring with unity has at least one regular element ideal: the trivial ideal R itself. Regular element ideals of commutative rings are essential ideals. In a semiprime right Goldie ring, the converse holds: essential ideals are all regular element ideals. (Lam 1999, p.342)
Since the product of two regular elements (=non-zerodivisors) of a commutative ring R is again a regular element, it is apparent that the product of two regular element ideals is again a regular element ideal. Clearly any ideal containing a regular element ideal is again a regular element ideal.
- Examples
- In an integral domain, every nonzero element is a regular element, and so every nonzero ideal is a regular element ideal.
- The nilradical of a commutative ring is composed entirely of nilpotent elements, and therefore no element can be regular. This gives an example of an ideal which is not a regular element ideal.
- In an Artinian ring, each element is either invertible or a zero divisor. Because of this, such a ring only has one regular element ideal: just R.
Von Neumann regular ideals
From the definition, it is clear that R is a von Neumann regular ring if and only if R is a von Neumann regular ideal. The following statement is a relevant lemma for von Neumann regular ideals:
Lemma: For a ring R and proper ideal J containing an element a, there exists and element y in J such that a=aya if and only if there exists an element r in R such that a=ara. Proof: The "only if" direction is a tautology. For the "if" direction, we have a=ara=arara. Since a is in J, so is rar, and so by setting y=rar we have the conclusion.
As a consequence of this lemma, it is apparent that every ideal of a von Neumann regular ring is a von Neumann regular ideal. Another consequence is that if J and K are two ideals of R such that J⊆K and K is a von Neumann regular ideal, then J is also a von Neumann regular ideal.
If J and K are two ideals of R, then K is von Neumann regular if and only if both J is a von Neumann regular ideal and K/J is a von Neumann regular ring[4].
Every ring has at least one von Neumann regular ideal, namely {0}. Futhermore, every ring has a maximal von Neumann regular ideal containing all other von Neumann regular ideals, and this ideal is given by
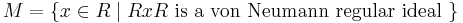 .
.
- Examples
- As noted above, every ideal of a von Neumann regular ring is a von Neumann regular ideal.
- It is well known that a local ring which is also a von Neumann regular ring is a division ring. Let R Be a local ring which is not a division ring, and denote the unique maximal right ideal by J. Then R cannot be von Neumann regular, but R/J, being a division ring, is a von Neumann regular ring. Consequently, J cannot be a von Neumann regular ideal, even though it is maximal.
- A simple domain which is not a division ring has the minimum possible number of von Neumann regular ideals: only the {0} ideal.
Quotient von Neumann regular ideals
If J and K are quotient von Neumann regular ideals, then so is J∩K.
If J⊆K are proper ideals of R and J is quotient von Neumann regular, then so is K. This is because quotients of R/J are all von Neumann regular rings, and an isomorphism theorem for rings establishing that R/K≅(R/J)/(J/K). In particular if A is any ideal in R the ideal A+J is quotient von Neumann regular if J is.
- Examples
- Every proper ideal of a von Neumann regular ring is quotient von Neumann regular.
- Any maximal ideal in a commutative ring is a quotient von Neumann regular ideal since R/M is a field. This is not true in general because for noncommutative rings R/M may only be a simple ring, and may not be von Neumann regular.
- Let R be a local ring which is not a division ring, and with maximal right ideal M . Then M is a quotient von Neumann regular ideal, since R/M is a division ring, but R is not a von Neumann regular ring.
- More generally in any semilocal ring the Jacobson radical J is quotient von Neumann regular, since R/J is a semisimple ring, hence a von Neumann regular ring.
References
- ^ Non-zerodivisors in commutative rings are called regular elements.
- ^ Burton, D.M. (1970) ``A first course in rings and ideals. Addison-Wesley. Reading, Massachusetts .
- ^ Jacobson 1956, p.6.
- ^ Goodearl 1991, p.2.
- Goodearl, K. R. (1991), von Neumann regular rings (2 ed.), Malabar, FL: Robert E. Krieger Publishing Co. Inc., pp. xviii+412, ISBN 0-89464-632-X, MR1150975
- Jacobson, Nathan (1956), Structure of rings, American Mathematical Society, Colloquium Publications, vol. 37, 190 Hope Street, Prov., R. I.: American Mathematical Society, pp. vii+263, MR0081264
- Irving Kaplansky (1969). Fields and Rings. The University of Chicago Press.
- Larsen, Max. D.; McCarthy, Paul J. (1971), Multiplicative theory of ideals, New York: Academic Press, pp. xiv+298, MR0414528
- Zhevlakov, K.A. (2001), "Modular ideal", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=m/m064450.htm